Answer for HW_14_15

1 HW 14

1.1 规则运动

根据角速度和欧拉角的关系直接计算可得

{\vec{ω}}_{本 体 系} = [\begin{matrix} \dot{φ} \sin θ \sin ψ + \dot{θ} \cos ψ \\ \dot{φ} \sin θ \cos ψ - \dot{θ} \sin ψ \\ \dot{φ} \cos θ + \dot{ψ} \end{matrix}] = [\begin{matrix} a \sin θ_{0} \sin (ψ_{0} + c t) \\ - a \sin θ_{0} \cos (ψ_{0} + c t) \\ a \cos θ_{0} + c \end{matrix}]

1.2 这是一道微改的考试原题

(2016) 五、(15 分) 质量为 $m$ , 半长轴 $a$ 、半短轴为 $b$ 的椭圆形匀质盘绕通过其中心且在盘平面内的固定轴 $e_{A O}$ 作匀速转动, 角速度为 $ω_{0}$ 。转轴与㮋圆半长轴的夹角为 $α$ , 转轴质量可以忽略。
(1) 求主转动惯量;
(2) 写出角速度在主轴系中的分量;
本题：(3) 写出匀质盘的转动动能.
原题：(3)' 求该椭圆盘所受到力矩。

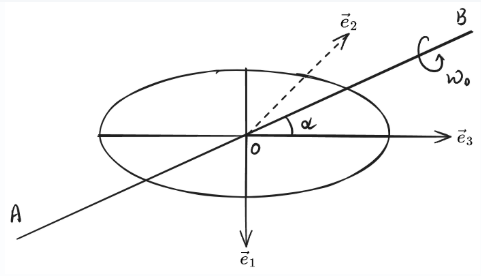
Drawing 2024-11-14 11.23.13.excalidraw

解：以椭圆盘中心 O 为原点，建立如图所示的主轴坐标系 (右手系)， $e_{1}$ 沿短轴方向， $e_{3}$ 沿长轴方向, $e_{2}$ 垂直纸面向里。转动角速度在此主轴系的分量为 $ω_{1} = - ω_{0} \sin α, ω_{2} = 0, ω_{3} = ω_{0} \cos α$ . 因为匀速转动, 所以 ${\dot{ω}}_{1} = {\dot{ω}}_{2} = {\dot{ω}}_{3} = 0$

(1) 直接计算给出

I_{1} = \iint ρ (y^{2} + z^{2}) d s = \frac{m}{π a b} \iint z^{2} d x d z = \frac{m}{π a b} \int_{- a}^{a} z^{2} d z \int_{- b \sqrt{1 - z^{2} / a^{2}}}^{b \sqrt{1 - z^{2} / a^{2}}} d x = \frac{2 m}{π a} \int_{- a}^{a} z^{2} \sqrt{1 - \frac{z^{2}}{a^{2}}} d z

令

\begin{matrix} z = acos \frac{θ}{2} \\ I_{1} = \frac{m a^{2}}{4 π} \int_{0}^{2 π} \frac{1 - \cos 2 θ}{2} d θ = \frac{m a^{2}}{4} \end{matrix}

类似地, $I_{3} = \frac{m b^{2}}{4}, I_{2} = I_{1} + I_{3} = \frac{m}{4} (a^{2} + b^{2})$ .

(2) 转动角速度在此主轴系的分量为

ω_{1} = - ω_{0} \sin α, ω_{2} = 0, ω_{3} = ω_{0} \cos α . 因 为 匀 速 转 动, 所 以 {\dot{ω}}_{1} = {\dot{ω}}_{2} = {\dot{ω}}_{3} = 0

(3) 在主轴系中，

T = \frac{1}{2} (I_{1} ω_{1}^{2} + I_{2} ω_{2}^{2} + I_{3} ω_{3}^{2})

得到

T = \frac{1}{8} m ω_{0}^{2} (a^{2} \sin^{2} α + b^{2} \cos^{2} α)

(3)' 由欧拉动力学方程

{\begin{cases} I_{1} {\dot{ω}}_{1} - (I_{2} - I_{3}) ω_{2} ω_{3} = N_{1} \\ I_{2} {\dot{ω}}_{2} - (I_{3} - I_{1}) ω_{3} ω_{1} = N_{2} \\ I_{3} {\dot{ω}}_{3} - (I_{1} - I_{2}) ω_{1} ω_{2} = N_{3} \end{cases}

可得 $N_{1} = N_{3} = 0, N_{2} = (I_{1} - I_{3}) ω_{3} ω_{1} = - \frac{m (a^{2} - b^{2})}{4} ω_{0}^{2} \sin α \cos α$ , 圆盘所受到的力矩大小为 $\frac{m (a^{2} - b^{2})}{4} ω_{0}^{2} \sin α \cos α$ ，方向为沿 $- e_{2}$ .

1.3 匀质圆柱

朗道：

接下来，微振动的拉氏量：

L = \frac{3}{4} μ (R - a)^{2} {\dot{φ}}^{2} + \frac{1}{2} μ g (R - a) φ^{2}

得到拉格朗日方程

\frac{3}{2} μ (R - a)^{2} \ddot{φ} - μ g (R - a) φ = 0

\ddot{φ} - \frac{2 g}{3 (R - a)} φ = 0

ω = \sqrt{\frac{2 g}{3 (R - a)}}

附鞠国兴解读：

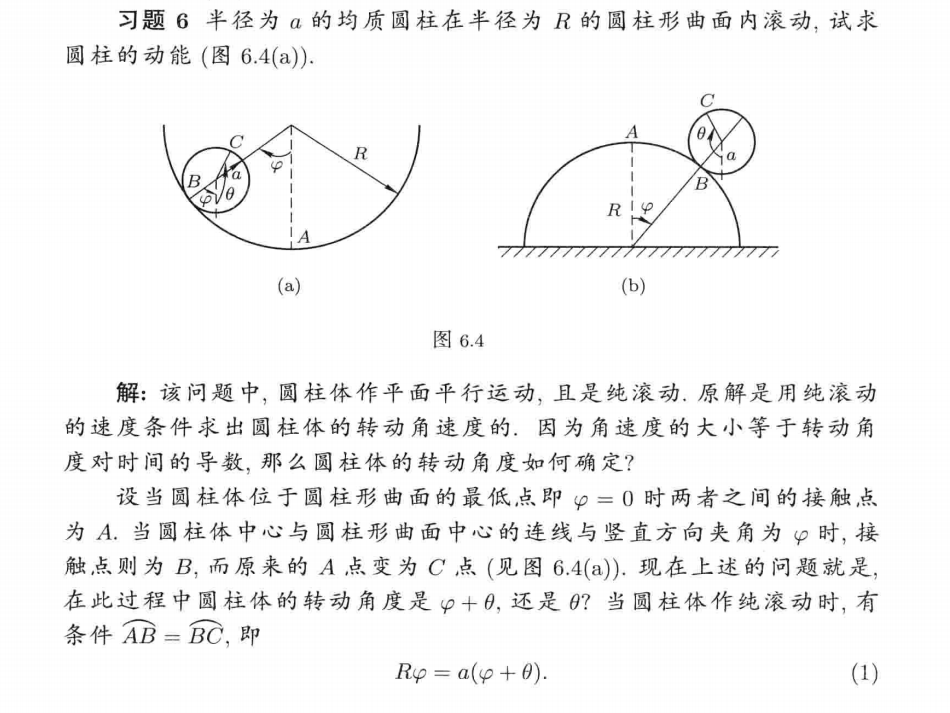
1.4 均质圆锥

朗道：

鞠国兴解读：

1.5 滚动的匀质圆锥

朗道：

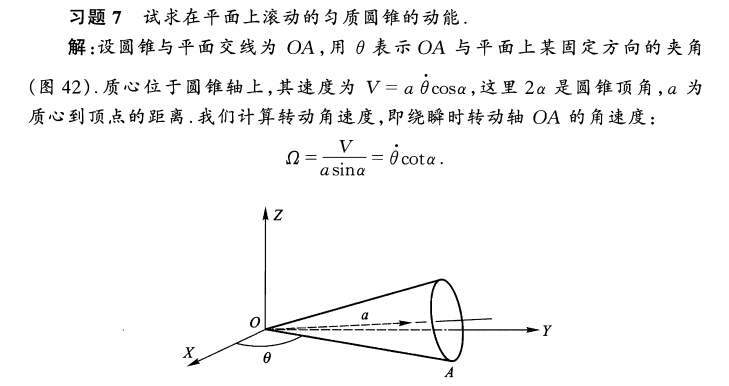
1.6 均质正方体

注意到

I = [\begin{matrix} A & B & B \\ B & A & B \\ B & B & A \end{matrix}], 其中 A = \frac{2}{3} M a^{2}, B = - \frac{1}{4} M a^{2}

则特征方程

| \begin{matrix} A - λ & B & B \\ B & A - λ & B \\ B & B & A - λ \end{matrix} | = 0

(A + 2 B - λ) | \begin{matrix} 1 & 1 & 1 \\ B & A - λ & B \\ B & B & A - λ \end{matrix} | = 0

(A + 2 B - λ) | \begin{matrix} 0 & 0 & 1 \\ 0 & A - λ - B & B \\ B - A + λ & B - A + λ & A - λ \end{matrix} | = 0

显然 $λ_{1} = A + 2 B$ ， $λ_{2, 3} = A - B$ ，即 $λ_{1} = \frac{1}{6} M a^{2}$ ， $λ_{2, 3} = \frac{11}{12} M a^{2}$ ，三个主轴方向：

v_{1} = \frac{1}{\sqrt{3}} [\begin{matrix} 1 \\ 1 \\ 1 \end{matrix}], v_{2} = \frac{1}{\sqrt{2}} [\begin{matrix} 1 \\ - 1 \\ 0 \end{matrix}], v_{3} = v_{1} \times v_{2} = \frac{1}{\sqrt{6}} [\begin{matrix} 1 \\ 1 \\ - 2 \end{matrix}]

2 HW 15

2.1 欧拉陀螺

(1)

回忆，在推导题目给定的(1)式时，假定了惯性系的 z 轴为守恒角动量 $\vec{L}$ 的方向，所以，在本体系中

\vec{L} = R_{ψ} R_{θ} R_{φ} [\begin{matrix} 0 \\ 0 \\ L \end{matrix}] = [\begin{matrix} L \sin θ \sin ψ \\ L \sin θ \cos ψ \\ L \cos θ \end{matrix}] = [\begin{matrix} I_{1} ω_{0} \cos (Ω t + α) \\ I_{1} ω_{0} \sin (Ω t + α) \\ I_{3} ω_{30} \end{matrix}]

这里

ω_{0} = \sqrt{ω^{2} - ω_{30}^{2}} = \frac{L \sin θ}{I_{1}}, Ω = - \dot{ψ} = c o n s t

所以

L = \frac{I_{3} ω_{30}}{\cos θ} = I_{1} \dot{φ}

或者

L = \frac{I_{3} ω_{30}}{\cos θ} = \frac{I_{3}}{\cos θ} \cdot \frac{I_{1}}{I_{1} - I_{3}} \dot{ψ}

(2)

对称欧拉陀螺是规则运动的，已知在本体系中

{\vec{ω}}_{B o d y} = [\begin{matrix} ω_{0} \cos (Ω t + α) \\ ω_{0} \sin (Ω t + α) \\ ω_{30} \end{matrix}]

记实验系坐标轴 x,y,z，将角速度在 z 轴投影得到

ω_{z} = \frac{\vec{ω} \cdot \vec{L}}{L} = \frac{I_{1} ω_{1}^{2} + I_{1} ω_{2}^{2} + I_{3} ω_{3}^{2}}{L} = \frac{I_{1} ω_{0}^{2} + I_{3} ω_{30}^{2}}{L} = L (\frac{\sin^{2} θ_{0}}{I_{1}} + \frac{\cos^{2} θ_{0}}{I_{3}})

或者直接计算

{\vec{ω}}_{L a b} = [\begin{matrix} \dot{ψ} \sin θ \sin φ + \dot{θ} \cos φ \\ - \dot{ψ} \sin θ \cos φ + \dot{θ} \sin φ \\ \dot{ψ} \cos θ + \dot{φ} \end{matrix}] = [\begin{matrix} L \sin θ_{0} \cos θ_{0} (\frac{1}{I_{3}} - \frac{1}{I_{1}}) \sin φ (t) \\ - L \sin θ_{0} \cos θ_{0} (\frac{1}{I_{3}} - \frac{1}{I_{1}}) \cos φ (t) \\ L (\frac{\sin^{2} θ_{0}}{I_{1}} + \frac{\cos^{2} θ_{0}}{I_{3}}) \end{matrix}]

2.2 共面性质

本体系中

\vec{ω} = [\begin{matrix} ω_{0} \cos α \\ ω_{0} \sin α \\ ω_{30} \end{matrix}], \vec{e_{z}} = [\begin{matrix} 0 \\ 0 \\ 1 \end{matrix}], \vec{L} = [\begin{matrix} I_{1} ω_{0} \cos α \\ I_{1} ω_{0} \sin α \\ I_{3} ω_{30} \end{matrix}], α = α (t)

所以

(\vec{ω} \times \vec{e_{z}}) \cdot \vec{L} = [\begin{matrix} ω_{0} \sin α \\ - ω_{0} \cos α \\ 0 \end{matrix}] \cdot [\begin{matrix} I_{1} ω_{0} \cos α \\ I_{1} ω_{0} \sin α \\ I_{3} ω_{30} \end{matrix}] = 0

所以三者共面。

2.3 均质盘旋转

2.4 这是一道真题

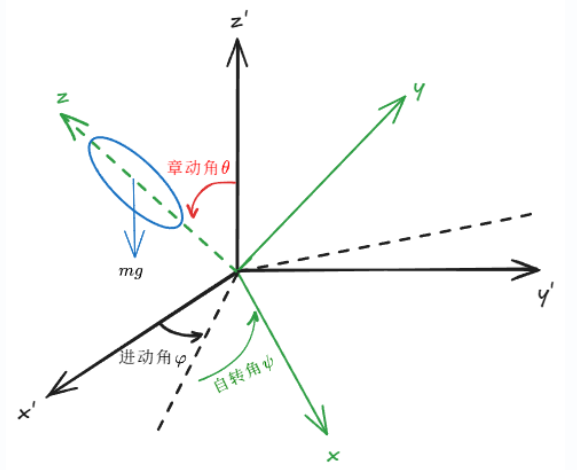
Drawing 2024-11-14 14.15.10.excalidraw

(1)

H = \frac{p_{θ}^{2}}{2 I_{1}} + V_{e f f} (θ), V_{e f f} (θ) = \frac{(p_{φ} - p_{ψ} \cos θ)^{2}}{2 I_{1} \sin^{2} θ} + \frac{p_{ψ}^{2}}{2 I_{3}} + m g l \cos θ

根据循环坐标得到运动积分

p_{ψ} = c o n s t, p_{φ} = c o n s t .

以及 H 不显含 t：

H \equiv E = c o n s t

(2)

\begin{matrix} S = - E t + p_{ϕ} ϕ + p_{ψ} ψ + W_{θ} (θ) \\ \frac{1}{2 I_{1}} {\frac{{(p_{ϕ} - p_{ψ} \cos θ)}^{2}}{\sin^{2} θ} + {(\frac{d W_{θ}}{d θ})}^{2}} + \frac{p_{ψ}^{2}}{2 I_{3}} + m g l \cos θ = E \\ \Rightarrow \frac{d W_{θ}}{d θ} = \sqrt{2 I_{1} (E - \frac{p_{ψ}^{2}}{2 I_{3}} - m g l \cos θ) - \frac{{(p_{ϕ} - p_{ψ} \cos θ)}^{2}}{\sin^{2} θ}} \\ \Rightarrow S = - E t + p_{ϕ} ϕ + p_{ψ} ψ + \int \sqrt{2 I_{1} (E - \frac{p_{ψ}^{2}}{2 I_{3}} - m g l \cos θ) - \frac{{(p_{ϕ} - p_{ψ} \cos θ)}^{2}}{\sin^{2} θ}} d θ \end{matrix}

运动积分：

ξ = \frac{\partial S}{\partial E} = - t + \int \frac{I_{1} d θ}{\sqrt{2 I_{1} (E - \frac{p_{ψ}^{2}}{2 I_{3}} - m g l \cos θ) - \frac{{(p_{ϕ} - p_{ψ} \cos θ)}^{2}}{\sin^{2} θ}}} \Rightarrow θ (t)

Q_{ϕ} = \frac{\partial S}{\partial p_{ϕ}} = ϕ - \int \frac{(p_{ϕ} - p_{ψ} \cos θ) / \sin^{2} θ}{\sqrt{2 I_{1} (E - \frac{p_{ψ}^{2}}{2 I_{3}} - m g l \cos θ) - \frac{(p_{ϕ} - p_{ψ} \cos θ)^{2}}{\sin^{2} θ}}} d θ \Rightarrow ϕ (θ)

Q_{ψ} = \frac{\partial S}{\partial p_{ψ}} = ψ - \int \frac{\frac{I_{1} p_{ψ}}{I_{3}} - \frac{(p_{ϕ} - p_{ψ} \cos θ) \cos θ}{\sin^{2} θ}}{\sqrt{2 I_{1} (E - \frac{p_{ψ}^{2}}{2 I_{3}} - m g l \cos θ) - \frac{(p_{ϕ} - p_{ψ} \cos θ)^{2}}{\sin^{2} θ}}} d θ \Rightarrow ψ (θ)

另一道类似的：

(2021) 五、(25 分）拉格朗日陀螺为在重力场中的对称刚体 $(I_{1} = I_{2} \neq I_{3})$ 。它的拉格朗日量为:

L = \frac{I_{1}}{2} ({\dot{θ}}^{2} + {\dot{φ}}^{2} \sin^{2} θ) + \frac{I_{3}}{2} (\dot{ψ} + \dot{φ} \cos θ)^{2} - m g l \cos θ

(1)根据 $L$ 的对称性，找出系统的三个守恒量并说明理由;
(2)根据刚体的欧拉动力学方程, 证明广义动量 $p_{φ}$ 和 $p_{ψ}$ 为运动积分。

(1) 拉格朗日量 $L$ 不显含时间, 因此哈密顿量 $H = E$ 为守恒量。另外, $ψ, φ$ 为循环坐标, 因此正则动量 $p_{ψ}, p_{φ}$ 为运动积分, 即:

\begin{matrix} \frac{I_{1}}{2} ({\dot{θ}}^{2} + {\dot{φ}}^{2} \sin^{2} θ) + \frac{I_{3}}{2} (\dot{ψ} + \dot{φ} \cos θ)^{2} - m g l \cos θ = E = const . \\ p_{ψ} = \frac{\partial L}{\partial \dot{ψ}} = I_{3} (\dot{ψ} + \dot{φ} \cos θ) = const . \\ p_{φ} = \frac{\partial L}{\partial \dot{φ}} = (I_{3} \cos^{2} θ + I_{1} \sin^{2} θ) \dot{φ} + I_{3} \dot{ψ} \cos θ = const \end{matrix}

(2) 力矩的方向显然同时垂直于刚体的 $z$ 轴和实验室系的 $z^{'}$ 方向, 因此,

N_{3} = 0, N_{3^{'}} = 0

根据欧拉动力学公式有:

I_{3} {\dot{ω}}_{3} - (I_{1} - I_{2}) ω_{1} ω_{2} = I_{3} {\dot{ω}}_{3} = 0

即

p_{ψ} = L_{3} = I_{3} ω_{3} = I_{3} (\dot{ψ} + \dot{φ} \cos θ) = const .

另外,

\frac{d}{d t} (L_{3^{'}}) = N_{3^{'}} = 0

易得：

p_{φ} = L_{3'} = (I_{3} \cos^{2} θ + I_{1} \sin^{2} θ) \dot{φ} + I_{3} \dot{ψ} \cos θ = const.

其中刚体绕实验室系的 $z^{'}$ 轴的转动惯量为:

I_{3'} = I_{3} \cos^{2} θ + I_{1} \sin^{2} θ

2.5 这也是一道考试原题

也可以由角动量的进动角速度 $Ω = ω_{0} = \frac{N}{J \sin θ} = \frac{N}{I_{3} ω_{0}}$ 得到,

N = ω_{0} \cdot I_{3} ω_{0} = \frac{1}{2} m r ω_{0}^{2} = N_{水 平 面 对 圆 盘 支 持 力} - m g

附 :

角动量进动和外力力矩的关系

对于 $z$ 方向力矩，不需要考虑，它只对角动量的自转起作用。只考虑垂直于 $z$ 方向的力矩 $M$ 。
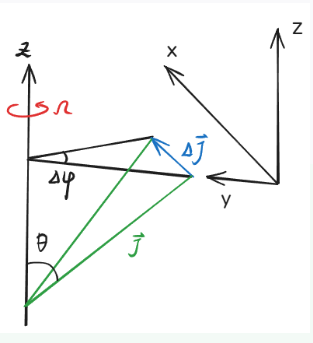
zz_figure/Pasted image 20251225153320.png
如图，角动量守恒:

Δ J = J s i n θ Δ φ = M Δ t \to Ω = \frac{Δ φ}{Δ t} = \frac{M}{J \sin θ}

可以发现有效力矩指向 $x$ 方向。进动周期:

T_{p} = \frac{2 π}{Ω}

2.6 这题作为第三小问考过

注意到

H = \frac{p_{θ}^{2}}{2 I_{1}} + V_{e f f} (θ), V_{e f f} (θ) = \frac{(p_{φ} - p_{ψ} \cos θ)^{2}}{2 I_{1} \sin^{2} θ} + \frac{p_{ψ}^{2}}{2 I_{3}} + m g l \cos θ

p_{θ} = I_{1} \dot{θ}

在 $θ = c o n s t$ 时， $\dot{φ} = \frac{\partial H}{\partial p_{φ}} = f (θ) = c o n s t$ 自动成立，所以条件只有 $p_{θ} \sim \dot{θ} = 0$ ，此时

E = {V_{e f f}}_{m i n}

即

\frac{d V_{e f f}}{d θ} = 0

必须有解。

一个圆锥密度均匀为 $ρ$ , 总质量 $M$ , 底部的圆半径为 $R$ , 高为 $h$ 。
(1). 求相对于圆雉顶点的主转动惯量 $I_{1}, I_{2}, I_{3}$ .
(2). 以圆雉顶点为固定点, 求重力场中, 该重对称陀螺的拉氏量及三个守恒量方程.
(3). 重对称陀螺也能均匀进动 (章动角 $θ$ 和进动角速度 $\dot{ϕ}$ 保持不变)。以圆锥顶点为固定点, 求该重对称陀螺可以均匀进动的角速度 $\dot{ϕ}$ , 并给出均匀进动的存在性条件

(1) 选取 $z$ 轴为垂直于底面的对称轴的坐标系, 原点在底面中心。得：

I_{1} = I_{2} = \frac{3}{20} M (R^{2} + 4 h^{2}), I_{3} = \frac{3}{10} M R^{2}

tips : 积分时使用平行轴定理

\begin{matrix} I_{1} = \int_{0}^{h} [\frac{1}{4} d m \cdot r^{2} + d m \cdot z^{2}] \\ d m = ρ π r^{2} d z, r = \frac{R}{h} z, M = \frac{1}{3} π R^{2} h \end{matrix}

(2) 刚体的质心高度 :

l = \frac{\int_{0}^{h} z \cdot r^{2} d z}{\int_{0}^{h} r^{2} d z} = \frac{3}{4} h

刚体的拉格朗日量为

L = \frac{I_{1}}{2} ({\dot{θ}}^{2} + {\dot{ϕ}}^{2} \sin^{2} θ) + \frac{I_{3}}{2} (\dot{ψ} + \dot{ϕ} \cos θ)^{2} - \frac{3}{4} m g h \cos θ

三个守恒量分别为:

\begin{matrix} E = \frac{I_{1}}{2} ({\dot{θ}}^{2} + {\dot{ϕ}}^{2} \sin^{2} θ) + \frac{I_{3}}{2} (\dot{ψ} + \dot{ϕ} \cos θ)^{2} + \frac{3}{4} m g h \cos θ \\ P_{ϕ} = \frac{\partial L}{\partial \dot{ϕ}} = (I_{1} \sin^{2} θ + I_{3} \cos^{2} θ) \dot{ϕ} + I_{3} \cos θ \dot{ψ} = const . \\ P_{ψ} = \frac{\partial L}{\partial \dot{ψ}} = I_{3} (\dot{ψ} + \dot{ϕ} \cos θ) = I_{3} ω_{3} = const \end{matrix}

(3) 解法一:

根据欧拉-拉格朗日方程, 得到 $θ$ 方向的运动方程为:

I_{1} \ddot{θ} = (I_{1} \cos θ {\dot{ϕ}}^{2} - I_{3} ω_{3} \dot{ϕ} + 3 M g h / 4) \sin θ = \frac{d V_{e f f}}{d θ}

均匀进动时, $\ddot{θ} = 0, θ = θ_{0}$ , 因此,

I_{1} \cos θ {\dot{ϕ}}^{2} - I_{3} ω_{3} \dot{ϕ} + 3 M g h / 4 = 0

这是关于 $\dot{ϕ}$ 的二次方程，方程有解的条件：

Δ = {(I_{3} ω_{3})}^{2} - 3 M g h I_{1} \cos θ_{0} \geq 0

即：

ω_{3} \geq \frac{\sqrt{3 M g h I_{1} \cos θ_{0}}}{I_{3}}

解法二 :

根据上面三个守恒量, 得到 $θ$ 方向的运动满足:

\begin{matrix} \frac{I_{1}}{2} {\dot{θ}}^{2} = E^{'} - V_{e f f} (θ) \\ E^{'} = E - \frac{P_{ψ}^{2}}{2 I_{3}} \\ V_{e f f} (θ) = \frac{{(P_{ϕ} - P_{ψ} \cos θ)}^{2}}{2 I_{1} \sin^{2} θ} + \frac{3}{4} m g h \cos θ \end{matrix}

均匀进动的条件为 $V_{e f f} (θ)$ 取极小值, 即:

\begin{matrix} E^{'} = V_{e f f} (θ_{0}) \\ \frac{d V_{e f f} (θ)}{d θ} | θ = θ_{0} = 0 \end{matrix}

令:

\begin{matrix} α = \frac{2 E^{'}}{I_{1}}, β = \frac{3 m g h}{2 I_{1}}, a = \frac{P_{ψ}}{I_{1}}, b = \frac{P_{ϕ}}{I_{1}}, u = c o s θ \\ {\dot{u}}^{2} = (1 - u^{2}) (α - β u) - (b - a u)^{2} \equiv f (u) \end{matrix}

另有:

\dot{ϕ} = \frac{(b - a u)}{1 - u^{2}}

由 $f (u_{0}) = 0$ , 得到:

α - β u_{0} = \frac{{(b - a u_{0})}^{2}}{(1 - u_{0}^{2})}

由 $f^{'} (u_{0}) = 0$ , 得到:

\frac{β}{2} = \frac{a (b - a u_{0})}{(1 - u_{0}^{2})} - \frac{u_{0} (α - β u_{0})}{(1 - u_{0}^{2})}

利用:

{\dot{ϕ}}_{0} = \frac{(b - a u_{0})}{1 - u_{0}^{2}}

得到：

\frac{β}{2} = a {\dot{ϕ}}_{0} - u_{0} {\dot{ϕ}}_{0}^{2}

这是关于 ${\dot{ϕ}}_{0}$ 的二次方程，方程有解的条件是：

Δ = a^{2} - 2 β u_{0} \geq 0

即：

ω_{3} \geq \frac{\sqrt{3 M g h \cos θ_{0} I_{1}}}{I_{3}}