Answer for HW_13

1 三维各向同性谐振子

本题的哈密顿量表示的是一个 3-D 各向同性的谐振子，因此轨道是一个椭圆，该椭圆所在的平面经过原点。很容易发现，直角坐标中三个坐标的变化周期比是 $1 : 1 : 1$ ，柱坐标中是 $T_{ρ} : T_{z} : T_{θ} = \frac{1}{2} : 1 : 1$ ，球坐标中是 $T_{r} : T_{θ} : T_{φ} = \frac{1}{2} : 1 : 1$ 。所以，结果可以直接猜到：

H = ω (J_{x} + J_{y} + J_{z}) = ω (2 J_{ρ} + J_{θ} + J_{z}) = ω (2 J_{r} + J_{θ} + J_{φ})

接下来是更严格的求解。

1.1 直角坐标

已知基本关系：

L = \frac{m}{2} ({\dot{x}}^{2} + {\dot{y}}^{2} + {\dot{z}}^{2}) - \frac{1}{2} m ω^{2} r^{2}

\vec{p} = \frac{\partial L}{\partial \dot{\vec{r}}} = m \dot{\vec{r}}

H = \frac{p^{2}}{2 m} + \frac{1}{2} m ω^{2} r^{2}

于是 $H - J$ 方程为

\frac{1}{2 m} [{(\frac{\partial S_{0}}{\partial x})}^{2} + {(\frac{\partial S_{0}}{\partial y})}^{2} + {(\frac{\partial S_{0}}{\partial z})}^{2}] + \frac{1}{2} m ω^{2} (x^{2} + y^{2} + z^{2}) = E

可以令 $S_{0} = S_{x} (x) + S_{y} (y) + S_{z} (z)$ ，代入上式，有

[\frac{1}{2 m} {(\frac{d S_{x}}{d x})}^{2} + \frac{1}{2} m ω^{2} x^{2}] + [\frac{1}{2 m} {(\frac{d S_{y}}{d y})}^{2} + \frac{1}{2} m ω^{2} y^{2}] + [\frac{1}{2 m} {(\frac{d S_{z}}{d z})}^{2} + \frac{1}{2} m ω^{2} z^{2}] = E

于是分离变量有

[\frac{1}{2 m} {(\frac{d S_{i}}{d x_{i}})}^{2} + \frac{1}{2} m ω^{2} x_{i}^{2}] = E_{i}, i = x, y, z

作用变量

J_{i} = \frac{1}{2 π} \oint p_{i} d x_{i}, p_{i} = \frac{\partial S}{\partial x_{i}} = \frac{d S_{i}}{d x_{i}} = \sqrt{2 m E_{i} - m^{2} ω^{2} x_{i}^{2}}

注意到取 ${(\frac{d S_{i}}{d x_{i}})}^{2} = 0$ ，可以得到运动范围 $x_{i} \in [- A_{i}, A_{i}], A_{i} = \sqrt{\frac{2 E_{i}}{m ω^{2}}}$ ，于是

J_{i} = \frac{1}{2 π} \cdot 2 \int_{- A_{i}}^{A_{i}} \sqrt{2 m E_{i} - m^{2} ω^{2} x_{i}^{2}} d x_{i} = \frac{E_{i}}{ω}, i = x, y, z

上面这个积分实际上就是 $[\frac{p_{i}^{2}}{2 m} + \frac{1}{2} m ω^{2} x_{i}^{2}] = E_{i}$ 这个相空间椭圆的面积 $S$ 除以 $2 π$ ，即： $J_{i} = \frac{1}{2 π} S = \frac{1}{2 π} \cdot π \sqrt{2 m E_{i} \cdot \frac{2 E_{i}}{m ω^{2}}} = \frac{E_{i}}{ω}$ 。所以新的哈密顿量为

H = ω (J_{x} + J_{y} + J_{z})

角频率

ω_{i} = \frac{\partial H}{\partial J_{i}} = ω, i = x, y, z

1.2 柱坐标

已知基本关系：

L = \frac{m}{2} ({\dot{ρ}}^{2} + ρ^{2} {\dot{θ}}^{2} + {\dot{z}}^{2}) - \frac{1}{2} m ω^{2} (ρ^{2} + z^{2})

\begin{aligned} p_{ρ} & = \frac{\partial L}{\partial \dot{ρ}} = m \dot{ρ} \\ p_{z} & = \frac{\partial L}{\partial \dot{z}} = m \dot{z} \\ p_{θ} & = \frac{\partial L}{\partial \dot{θ}} = m ρ^{2} \dot{θ} \end{aligned}

H = \frac{1}{2 m} (p_{ρ}^{2} + \frac{p_{θ}^{2}}{ρ^{2}} + p_{z}^{2}) + \frac{1}{2} m ω^{2} (ρ^{2} + z^{2})

于是 $H - J$ 方程为

\frac{1}{2 m} {(\frac{\partial S_{0}}{\partial ρ})}^{2} + \frac{1}{2} m ω^{2} (ρ^{2} + z^{2}) + \frac{1}{2 m ρ^{2}} {(\frac{\partial S_{0}}{\partial θ})}^{2} + \frac{1}{2 m} {(\frac{\partial S_{0}}{\partial z})}^{2} = E

可以令 $S_{0} = p_{θ} θ + S_{ρ} (ρ) + S_{z} (z)$ ，代入上式，分离变量有

\frac{d S_{θ}}{d θ} \equiv p_{θ}

\frac{1}{2} m ω^{2} z^{2} + \frac{1}{2 m} {(\frac{d S_{z}}{d z})}^{2} = E_{z}

\frac{1}{2} m ω^{2} ρ^{2} + \frac{p_{θ}^{2}}{2 m ρ^{2}} + \frac{1}{2 m} {(\frac{d S_{ρ}}{d ρ})}^{2} = E_{ρ}

作用量

J_{θ} = \frac{1}{2 π} \oint p_{θ} d θ = p_{θ}

J_{z} = \frac{1}{2 π} \oint p_{z} d z = \frac{E_{z}}{ω}

\begin{aligned} J_{ρ} & = \frac{1}{2 π} \oint p_{ρ} d ρ \\ = \frac{1}{π} \int_{ρ_{m i n}}^{ρ_{m a x}} \sqrt{2 m E_{ρ} - m^{2} ω^{2} ρ^{2} - \frac{p_{θ}^{2}}{ρ^{2}}} d ρ \\ = \frac{E_{ρ}}{2 ω} - \frac{| J_{θ} |}{2} \end{aligned}

最后一个积分其实可以与 $ρ_{m i n, m a x}$ 无关，详见[[#附录%]]。于是

H = E_{ρ} + E_{z} = ω (2 J_{ρ} + | J_{θ} | + J_{z})

ω_{i} = \frac{\partial H}{\partial J_{i}} = 2 ω, ω \cdot sign (J_{θ}), ω, i = ρ, θ, z

1.3 球坐标

已知基本关系：

L = \frac{m}{2} ({\dot{r}}^{2} + r^{2} {\dot{θ}}^{2} + r^{2} {\dot{φ}}^{2} \sin^{2} θ) - V (r, θ, φ), V (r) = \frac{1}{2} m ω^{2} r^{2}

\begin{aligned} p_{r} & = \frac{\partial L}{\partial \dot{r}} = m \dot{r} \\ p_{θ} & = \frac{\partial L}{\partial \dot{θ}} = m r^{2} \dot{θ} \\ p_{φ} & = \frac{\partial L}{\partial \dot{φ}} = m r^{2} \dot{φ} \sin^{2} θ \end{aligned}

H = \dot{r} p_{r} + \dot{θ} p_{θ} + \dot{φ} p_{φ} - L = \frac{1}{2 m} (p_{r}^{2} + \frac{p_{θ}^{2}}{r^{2}} + \frac{p_{φ}^{2}}{r^{2} \sin^{2} θ}) + V (r, θ, φ)

于是 $H - J$ 方程为

\frac{1}{2 m} {(\frac{\partial S_{0}}{\partial r})}^{2} + \frac{1}{2} m ω^{2} r^{2} + \frac{1}{2 m r^{2}} {(\frac{\partial S_{0}}{\partial θ})}^{2} + \frac{1}{2 m r^{2} \sin^{2} θ} {(\frac{\partial S_{0}}{\partial φ})}^{2} = E

可以令 $S_{0} = p_{φ} φ + S_{r} (r) + S_{θ} (θ)$ ，代入上式，分离变量有

\frac{d S_{φ}}{d φ} \equiv p_{φ}

{(\frac{d S_{θ}}{d θ})}^{2} + \frac{p_{φ}^{2}}{\sin^{2} θ} = L^{2}

\frac{1}{2 m} {(\frac{d S_{r}}{d r})}^{2} + \frac{1}{2} m ω^{2} r^{2} + \frac{L^{2}}{2 m r^{2}} = E

作用量

J_{φ} = \frac{1}{2 π} \oint p_{φ} d φ = p_{φ}

\begin{aligned} J_{θ} & = \frac{1}{2 π} \oint p_{θ} d θ \\ = \frac{1}{π} \int_{θ_{m i n}}^{θ_{m a x}} \sqrt{L^{2} - \frac{p_{φ}^{2}}{\sin^{2} θ}} d θ \\ = \frac{1}{π} \int_{\arcsin | \frac{p_{φ}}{L} |}^{π - \arcsin | \frac{p_{φ}}{L} |} \sqrt{L^{2} - \frac{p_{φ}^{2}}{\sin^{2} θ}} d θ \\ = L - | p_{φ} | \end{aligned}

J_{r} = \frac{1}{2 π} \oint p_{r} d r = \frac{1}{π} \int_{r_{m i n}}^{r_{m a x}} \sqrt{2 m E + 2 m^{2} ω^{2} r^{2} - \frac{L^{2}}{r^{2}}} d r = - 2 π i (R e s (0) + R e s (\infty)) = \frac{E}{2 ω} - \frac{L}{2}

最后一个积分的计算方式和柱坐标的 $J_{ρ}$ 类似。就得到

H = E = ω (2 J_{r} + J_{θ} + | J_{φ} |)

ω_{i} = \frac{\partial H}{\partial J_{i}} = 2 ω, ω, ω \cdot sign (J_{φ}), i = r, θ, φ

2 位力定理

直接计算：

\begin{aligned} I_{r} + I_{θ} & = \int m \dot{r} d r + \int m r^{2} \dot{θ} d θ \\ = \int_{0}^{T} (m {\dot{r}}^{2} + m r^{2} {\dot{θ}}^{2}) d t, T 为 运 动 周 期 \\ = 2 \int_{0}^{T} E_{k} d t, E_{k} 为 动 能 \\ = 2 T \cdot \frac{1}{T} \int_{0}^{T} E_{k} d t = 2 T ⟨ E_{k} ⟩ \end{aligned}

根据位力定理， $⟨ E_{k} ⟩ = - \frac{1}{2} ⟨ V ⟩$ ，所以

\begin{aligned} I_{r} + I_{θ} & = - T ⟨ V ⟩ \\ = \int_{0}^{T} \frac{k}{r} d t \end{aligned}

成立。

3 平面谐振子

3.1

I_{i} = \frac{1}{2 π} \oint p_{i} d x = \frac{1}{2 π} \int_{0}^{T_{i}} ω_{i} {\dot{x_{i}}}^{2} d t, i = x, y

所以

2 ⟨ E_{k} ⟩ = 2 π (\frac{I_{x}}{T_{x}} + \frac{I_{y}}{T_{y}})

根据位力定理

⟨ V ⟩ = ⟨ E_{k} ⟩

所以

E \equiv ⟨ V ⟩ + ⟨ E_{k} ⟩ = 2 π (\frac{I_{x}}{T_{x}} + \frac{I_{y}}{T_{y}})

3.2

ω_{i} = \frac{\partial E}{\partial I_{i}} = \frac{2 π}{T_{i}} = {\dot{φ}}_{i}, i = x, y

\Rightarrow φ_{i} = ω_{i} t + φ_{i 0}

\Rightarrow E = ω_{x} I_{x} + ω_{y} I_{y} = \frac{1}{2} m ω_{x}^{2} A_{x}^{2} + \frac{1}{2} m ω_{y}^{2} A_{y}^{2} \Rightarrow A_{i} = \sqrt{\frac{2 I_{i}}{m ω_{i}}}

所以

x_{i} = A_{i} \cos (ω_{i} t + φ_{i 0}) = \sqrt{\frac{2 I_{i}}{m ω_{i}}} \cos φ_{i}, i = x, y

3.3

如上，代入 $φ_{i} = ω_{i} t + φ_{i 0}$ 即可。

3.4

这是一个李萨如图形。

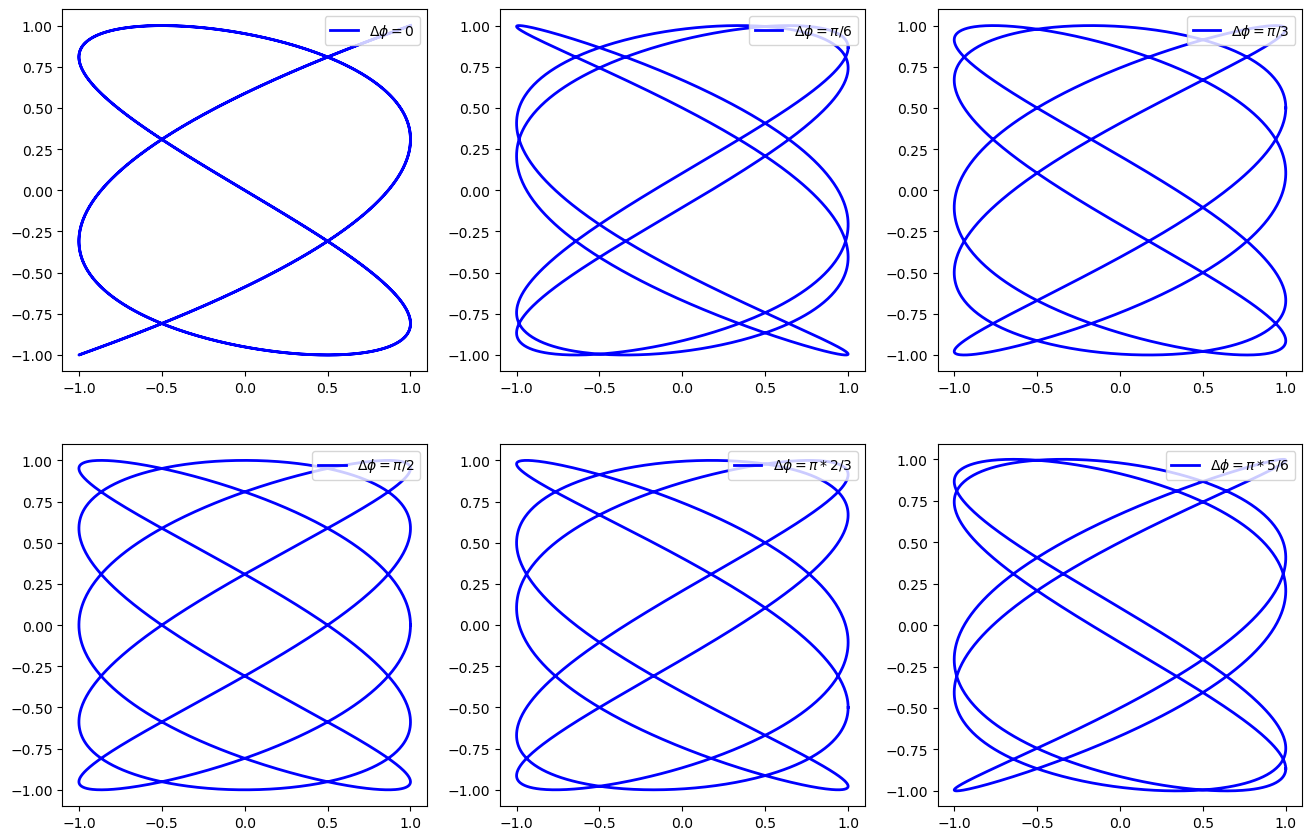
4 变长单摆

E = \frac{1}{2} m l^{2} {\dot{θ}}^{2} - m g l \cos θ \sim \frac{1}{2} m l^{2} {\dot{θ}}^{2} + \frac{1}{2} m g l θ^{2} = \frac{p_{θ}^{2}}{2 m l^{2}} + \frac{1}{2} m g l θ^{2}

作用量

J = \frac{1}{2 π} \oint p_{θ} d θ = \frac{1}{2 π} \cdot π \sqrt{2 m l^{2} E \cdot \frac{2}{m g l} E} = E \sqrt{\frac{l}{g}}

得到

E \sqrt{l} \equiv J \sqrt{g}

为绝热/浸渐不变量。

附录%

来处理这个丑陋的积分

J_{ρ} = \frac{1}{2 π} \oint p_{ρ} d ρ = \frac{1}{2 π} \oint \sqrt{2 m E_{ρ} - \frac{J_{θ}^{2}}{ρ^{2}} - m^{2} ω^{2} ρ^{2}} d ρ

令 $u = ρ^{2}$ ， $d ρ = \frac{d u}{2 \sqrt{u}}$ ：

\begin{aligned} J_{ρ} & = \frac{1}{2 π} \oint \sqrt{2 m E_{ρ} - \frac{J_{θ}^{2}}{u} - m^{2} ω^{2} u} \frac{d u}{2 \sqrt{u}} \\ = \frac{1}{4 π} \int_{u_{1}}^{u_{2}} \frac{\sqrt{- m^{2} ω^{2} u^{2} + 2 m E_{ρ} u - J_{θ}^{2}}}{u} d u \end{aligned}

设被积函数为 $f (u) = \frac{\sqrt{R (u)}}{u}$ ， $R (u) = - m^{2} ω^{2} u^{2} + 2 m E_{ρ} u - J_{θ}^{2}$ ，上式中 $u_{1, 2}$ 是 $R (u) = 0$ 的两个正实根，因此积分路径是复平面上包裹 $u_{1, 2}$ 连线 (即割线) 的闭合曲线。根据留数定理，包裹割线的回路积分等于包裹复平面上除割线以外所有奇点（原点 $u = 0$ 和无穷远点 $u = \infty$ ）留数之和的负值：

J_{ρ} = \frac{1}{4 π} \cdot (- 2 π i) [Res (f, 0) + Res (f, \infty)] = - \frac{i}{2} [Res (f, 0) + Res (f, \infty)]

在 $u \to 0$ 附近，展开 $\sqrt{R (u)}$ ：

\sqrt{R (u)} = \sqrt{- J_{ϕ}^{2} + 2 m E_{ρ} u - m^{2} ω^{2} u^{2}} = \sqrt{- J_{ϕ}^{2}} \sqrt{1 - (\frac{2 m E_{ρ}}{J_{θ}^{2}} u + O (u^{2}))}

为保证积分路径的相位正常，需要改写根号为

\sqrt{R (u)} = e^{\frac{ϕ_{1} + ϕ_{2}}{2}} \sqrt{- J_{θ}^{2} + 2 m E_{ρ} u - m^{2} ω^{2} u^{2}}, ϕ_{i} = a r g (u - u_{i})

当积分路径为正常地沿实轴 $u_{1} \to u_{2}$ 积分时，相位 $\frac{ϕ_{1} + ϕ_{2}}{2} = \frac{- π + π}{2} = 0$ 。注意这里不能选用根号的另一个分支 $\frac{ϕ_{1} + ϕ_{2}}{2} + π$ ，这会令积分得到的 $J_{ρ} < 0$ ，不符合物理意义，因为 $J_{ρ} = \frac{1}{2 π} \oint p_{ρ} d ρ$ 为相空间中闭合轨迹的面积，须大于 0。

采用留数和上述积分围道时，在 $u \to 0$ 附近得到

f (u) = \frac{| J_{θ} |}{u} (1 - \frac{m E_{ρ}}{J_{θ}^{2}} u + O (u^{2})) e^{\frac{ϕ_{1} + ϕ_{2} + π}{2}}

此时 $ϕ_{i} = a r g (0 - u_{i}) = π$ ，即 $e^{\frac{ϕ_{1} + ϕ_{2} + π}{2}} = - i$ ，因此，

Res (f, 0) = - i | J_{θ} |

在 $u \to \infty$ 附近：

\begin{aligned} \sqrt{R (u)} & = \sqrt{- m^{2} ω^{2} u^{2} (1 - \frac{2 m E_{ρ}}{m^{2} ω^{2} u} + \frac{J_{θ}^{2}}{m^{2} ω^{2} u^{2}})} \\ = m ω u {(1 - \frac{2 E_{ρ}}{m ω^{2} u} + O (\frac{1}{u^{2}}))}^{1 / 2} e^{\frac{ϕ_{1} + ϕ_{2} + π}{2}} \end{aligned}

此时

\begin{aligned} f (\frac{1}{u}) = u \sqrt{R (\frac{1}{u})} & \approx m ω {(1 - \frac{2 E_{ρ}}{m ω^{2}} u + O (u^{2}))}^{1 / 2} e^{\frac{ϕ_{1} + ϕ_{2} + π}{2}} \\ \approx - i m ω (1 + \frac{E_{ρ} u}{m ω^{2}}) \end{aligned}

于是

Res (f (u), \infty) = - Res (\frac{f (\frac{1}{u})}{u^{2}}, 0) = \frac{i E_{ρ}}{ω}

将两个留数代回 $J_{ρ}$ 的公式：

\begin{array}{r} J_{ρ} = - \frac{i}{2} (- i | J_{θ} | + \frac{i E_{ρ}}{ω}) = - \frac{1}{2} | J_{θ} | + \frac{E_{ρ}}{2 ω} \end{array}

这就是积分的最终结果。你也可以尝试用实积分求解，会得到相同的答案。