1 引力透镜
定义光程泛函 为:
其中 A、B 是光的起点和终点,费马原理指的是,所有连接 A、B 的可能曲线中,只有满足光程的变分为零才是光线走的路径,即:
在本题中,折射率是球对称的,光线始终在一个平面传播,可以采取极坐标:
代入拉格朗日方程 得到:
这是一个光学守恒量,记为 J,,称为光学角动量。在无穷远处, ,因为光线始终在一个平面传播,所以弧长微分满足:
代入 得到:
计算光线从无穷远来到近日点 ,再回到无穷远的总角度变化 ,有:
由 ,可得:
使用变量代换 ,则 ,于是:
代入 ,化为:
注意,最终的偏折角是 ,减去 是因为在没有引力时,偏折角是 而不是 0。所以偏折角:
法二从三维情形出发,这只是为了展示光线传播方程。将弧长微分 ds 改写为:
显然 等于 1,但是不妨碍我们把 凑成一个参数。于是光程可表示:
代入 Euler-Lagrange 方程 ,可以得到
也就是光线传播方程:
在本题中,折射率是球对称的,光线始终在一个平面传播,入射光线在无穷远处,瞄准半径为 。此时 只有径向分量(因为球对称,折射率只有径向梯度),于是
这是光学角动量(守恒),剩余的步骤和法一一致。
2 最小回转面
曲线绕 x 轴旋转的表面积为
代入 Euler-Lagrange 方程 并化简得到:
这正是悬链线方程,解为 。
3 修正最速降
设 v 是沿着这条曲线的速率,则降落一段弧长 所需的时间为 ,其中
运动所需时间为
令 ,则 ,,代入 Euler-Lagrange 方程中得到
这和课本(秦敢那本)第 20 页方程(16)差一个平移,令 ,则最终可得最速落径的参数方程
其尖端点的高度要高出 。
4 圆滚线
4.1 (a)
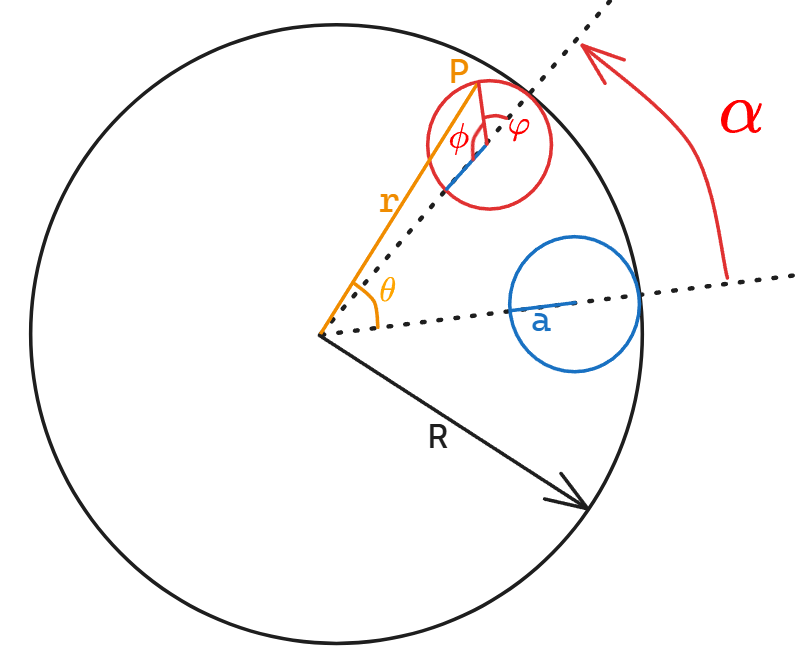
选取参量如下图所示
那么拉格朗日量可以写作:
代入拉格朗日方程得到:
正是简谐振动方程,。
4.2 (b)
还是先把所费的时间写成泛函形式:
第二个等号用到了单位质量物体的能量守恒 。于是拉氏量:
代入拉格朗日-欧拉方程 得到:
,积分得到(2)式。取 得到(3)式。
4.3 (c)
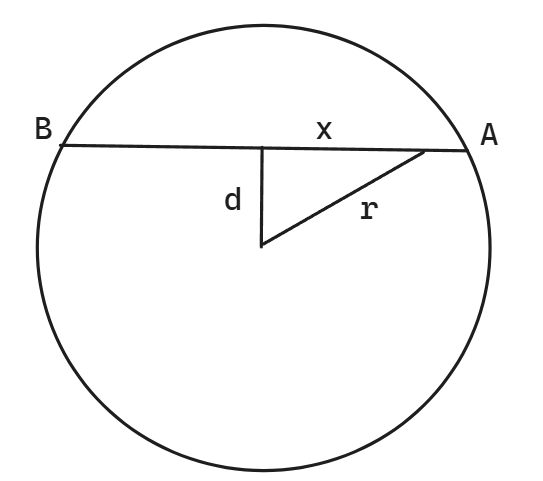
把(4)代入(2)就得到(6),反解(4)得到(5)。接下来看为什么(5)和(6)描述圆内滚轮线(现在变成了纯几何问题)。首先命名参量如下图:
根据几何关系,有:
注意图中 。以及再根据几何关系:
即(6)式。
4.4 (d)
由(5)可得:
由(6)可得:
根据 :
上式联立单位质量物体的能量守恒 得到
将(1)代入上式得到
将本小题一开始得到的(4.1)代入上式,并用(4.2)将 替换为 ,得到:
合肥到北京的纬度差 ,让滚轮转一圈那么 得到 ,于是
5 测地线
5.1 (a)
平面内的线元 ,则 ,对其求极值。令 ,则
代入欧拉方程 中,即 ,所以
正是直线。
5.2 (b)
柱面的线元
则 ,对其求极值.令 ,则
代入欧拉方程 中,即 ,所以
即螺旋线。
5.3 (c)
在每个点的邻域里,两者都是欧氏空间,即局部欧氏空间。
6 GR测地线
6.1 (a)
(10)式给出我们需要的拉氏量:
表示代入拉格朗日方程 ,利用 ,注意度规是坐标 的函数,有
以及
代入拉格朗日方程得到:
在最后一个等号中,使用了指标替换,第一项 ,第二项 ,因为都是缩并的指标,所以只是相当于给指标换了个名字。结合克里斯托费尔符号定义:
最终得测地线方程:
两边同时乘 可以得到
6.2 (b)
狭义相对论的闵氏空间中,度规是常数,所以联络为 0,测地线退化成:
即:
即
也就是直线。

